Fertility. Methods
Statistics Greenland
17 jan 2020
.
.
.
Age-specific fertility rates
Age-specific fertility rates for all birth orders combined and by birth order for the period 1994–2018 for Greenland are calculated on the basis of the official published live birth counts and population estimates (the de jure population).
Statistics Greenland combines 2 sources of information a) The Central Population Register(cpr.dk 1) and b) Birth certificates2 in cc to the National Board of Health in Nuuk
Everybody living in Greenland is assigned a 10-digit PIN(personal indentification number, danish: CPR) by birth or immigration. The system was introduced in Denmark in 1968, and from 1972 the same system was used in Greenland. All public administration uses the PIN.
For socioeconomic statistics this implys, that all administrative gathered information can be combined nationwide on all individuals with extremly high accuracy. Demographic measures can be calculated from microlevel using exact days.
The official aggregated tables on births are published in the StatBank of Statistics Greenland http://bank.stat.gl.
Full population account is also accessible in the statbank, at detailed Lexis-triangles level
Measures presented here are the most simple version of APC (Age, Period, Cohort) namely Age_Period as population exposures for a given age group are calculated as an average of population estimates for 1st January of a given year and the following year. As in this Lixes diagram:
if(!require(LexisPlotR)){install.packages("LexisPlotR")}
library(LexisPlotR)
lexis <- lexis_grid(year_start = 2015, year_end = 2020, age_start = 22, age_end = 25)
polygons <- data.frame(group = c(1, 1, 1, 1),
x = c("2017-01-01", "2017-01-01", "2018-01-01", "2018-01-01"),
y = c(23, 24, 24, 23))
lexis_polygon(lg = lexis, x = polygons$x, y = polygons$y, group = polygons$group)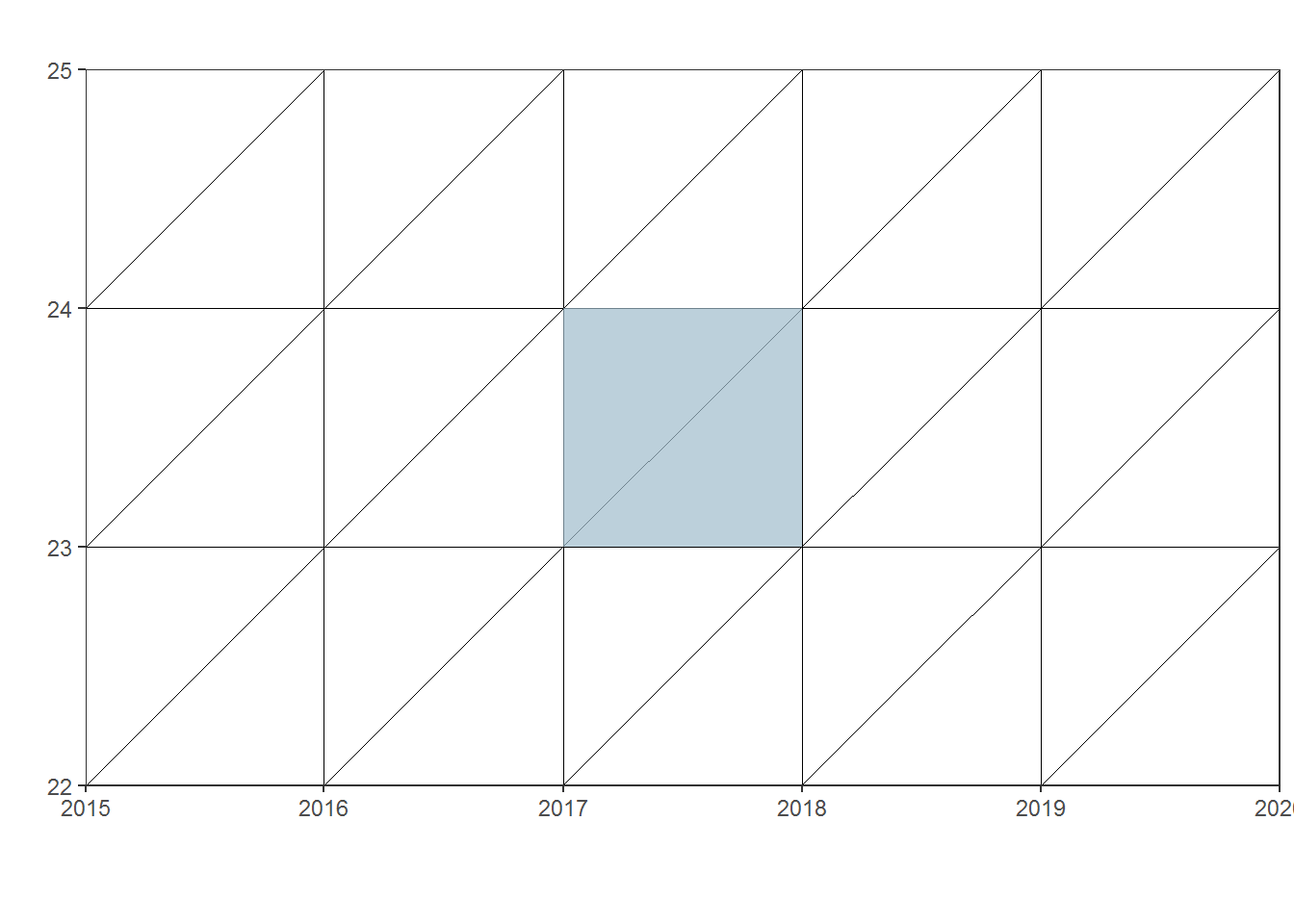
Births
Live births, 1994–: Data downloaded on: 23 juni, 2020
On parity, the mothers ages are published from ≤14 to 49+, specified by one-year age groups. Birth order ranges from 1 through 8+. As can be seen in http://bank.stat.gl/BEEBBP
if(!require(tidyverse)){install.packages("tidyverse")}
library(tidyverse)
if(!require(pxweb)){install.packages("pxweb")}
library(pxweb)
# PXWEB query & Download
px_data <-
pxweb_get(url = "http://bank.stat.gl/api/v1/en/Greenland/BE/BE10/BE1001/BE100120/BEXBBP.px",
query = list("mothers place of birth"=c("*"),
"mothers age"=c("*"),
"parity"=c("*"),
"time"=c("*"))
)
# Convert to data.frame
BIRTHS_pxw <- as.data.frame(px_data, column.name.type = "text", variable.value.type = "code")%>%
as_tibble()
BIRTHS = BIRTHS_pxw %>%
spread('time','Livebirth')
rm(px_data, BIRTHS_pxw)Female Population
Female population, 1994–: Data downloaded on: 23 juni, 2020
Annual population estimates are publish early February every year and population exposures for a given age group are calculated as an average of population estimates for 1st January of a given year and the following year.
Table can be found on http://bank.stat.gl/BEEST1
Alternatively it is also possible to find tables on mid-year population in the Statbank. Mid-year population is higher than January 1.st
if(!require(tidyverse)){install.packages("tidyverse")}
library(tidyverse)
if(!require(pxweb)){install.packages("pxweb")}
library(pxweb)
# PXWEB query & Download
px_data <-
pxweb_get(url = "http://bank.stat.gl/api/v1/en/Greenland/BE/BE01/BE0120/BEXST1.PX",
query = list("place of birth"=c("N","S"),
"gender"=c("K"),
"age"=c("*"),
"time"=c("*"))
)
# Convert to data.frame
POP_F_pxw <- as.data.frame(px_data, column.name.type = "text", variable.value.type = "code")%>%
as_tibble()
#
POP_F = POP_F_pxw %>%
spread('time','Population January 1st')
rm(px_data, POP_F_pxw)Calculations
Age-specific fertility rates calculated on on-year age groups for a small population, as Greenland, will show large fluctuations from one year to the next.
For each age, x, 14 - 49 a rate is calculated as:
where B is Livebirth and P i Population estimate.
In 2017 the age-specific fertilityrate for greenlandic born women was: 49/398.5 = 0.122961
if(!require(LexisPlotR)){install.packages("LexisPlotR")}
library(LexisPlotR)
lexis2 <- lexis_grid(year_start = 2015, year_end = 2020, age_start = 22, age_end = 25)
# Create a data.frame that contains the labels
labels <- data.frame(
x = c(
as.Date("2016-11-01"),
as.Date("2017-05-15"),
as.Date("2017-05-15"),
as.Date("2017-07-01"),
as.Date("2018-03-01")
),
y = c(
23.5,
23.7,
23.4,
23.2,
23.5
),
label = c(
"395",
"birth: 49",
"exposure:",
"398.5=(395+402)/2",
"402"
)
)
# Use geom_text to plot the labels
lexis2 + geom_text(aes(x = labels$x, y = labels$y, label = labels$label))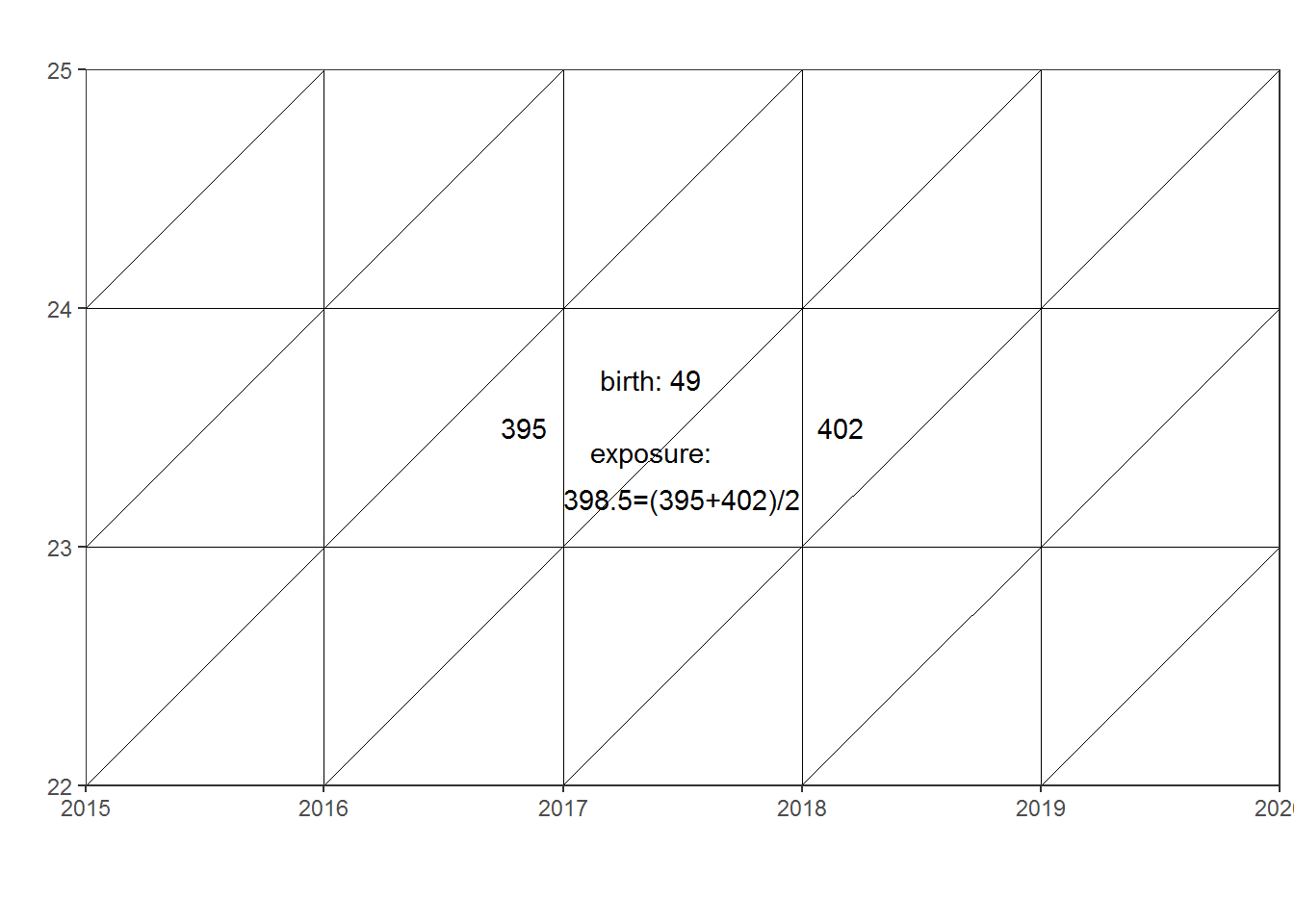
Age-specific fertility rates calculated on one-year age groups for a small population, as Greenland, will show large fluctuations from one year to the next.
Here age 23 is plottet from 1994 and onward:
BIRTHS1 <- BIRTHS
BIRTHS1 <- BIRTHS1 %>% filter(BIRTHS1$`mothers place of birth` == "N")
BIRTHS1 <- subset(BIRTHS1, select = -`mothers place of birth`)
BIRTHS1$parity <- as.numeric(as.character(BIRTHS1$parity))
BIRTHS1$parity[BIRTHS1$parity>1]<-1
BIRTHS2<-subset(aggregate(BIRTHS1[,3:27],
list(age=BIRTHS1$`mothers age`,BIRTHS1$parity),sum), select=-Group.2)
rm(BIRTHS1)
POP_F <- POP_F %>% filter(POP_F$`place of birth` == "N")
POP_F <- select(POP_F, age,`1994`,`1995`,`1996`,`1997`,`1998`,`1999`,
`2000`,`2001`,`2002`,`2003`,`2004`,`2005`,`2006`,`2007`,`2008`,`2009`,`2010`,
`2010`,`2011`,`2012`,`2013`,`2014`,`2015`,`2016`,`2017`,`2018`,`2019`)
POP_F$age <- as.numeric(as.character(POP_F$age))
POP_F <- filter(POP_F, age > 13, age < 50)
EXP<-POP_F[,1:27]
EXP[,2:26]<-(POP_F[,2:26]+POP_F[,3:27])/2
EXP$age<-as.numeric(as.character(EXP$age))
EXP<-POP_F[,1:ncol(POP_F)]
d1 <- EXP[,2:ncol(POP_F)-1]
d2 <-POP_F[,3:ncol(POP_F)-1]
d3 <- POP_F[,3:ncol(POP_F)]
EXP[,3:ncol(POP_F)-1]<-(POP_F[,3:ncol(POP_F)-1]+POP_F[,3:ncol(POP_F)])/2
EXP$age<-as.numeric(as.character(EXP$age))
ASFR2<-BIRTHS2
ASFR2[,2:26]<-ASFR2[,2:26]/EXP[,2:26]
ASFR2$age<-as.numeric(as.character(ASFR2$age))
TFR2<-colSums(ASFR2[,2:26])
ASFR3<-ASFR2
ASFR3[,2:26]<-ASFR3[,2:26]*ASFR3[,1]
MAB2<-colSums(ASFR3[,2:26])/TFR2+0.5
ASFR223 <- filter(ASFR2, age == '23')
ASFR23<-colSums(ASFR223[,2:26])
plot(ASFR23, type="l", xlab="time", ylab="rate")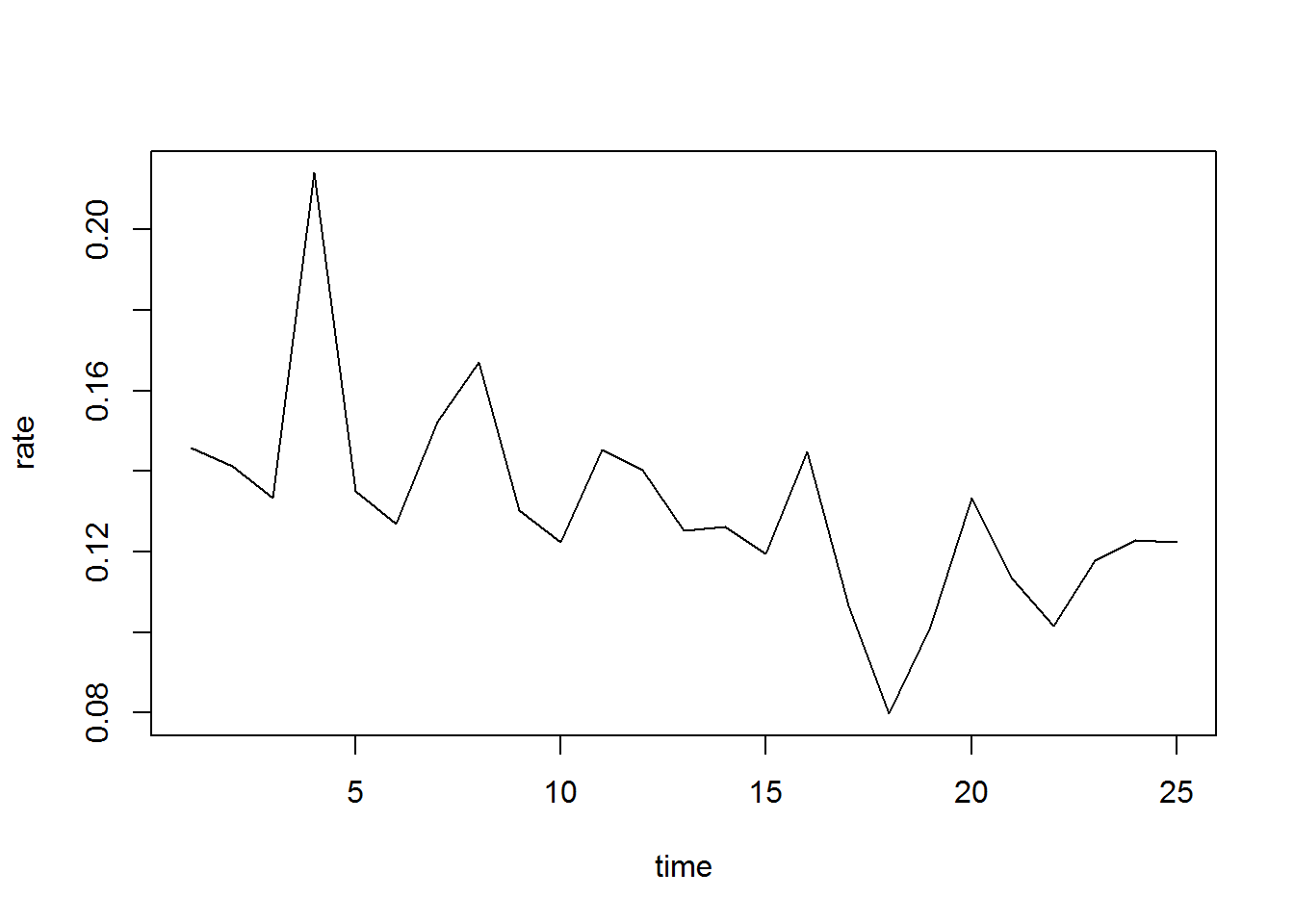
ylab('rate')## $y
## [1] "rate"
##
## attr(,"class")
## [1] "labels"ASFR2%>%
gather(time,value,-age)%>%
filter(time=='2018')%>%
ggplot(aes(x=age,y=value))+
geom_line()+
geom_smooth() +
labs(x = "age", y = "rate",
title = "Age-specific fertility rates, 2018",
subtitle = "annual flucturations due to a very small population",
caption = "Statistics Greenland") +
theme_statgl()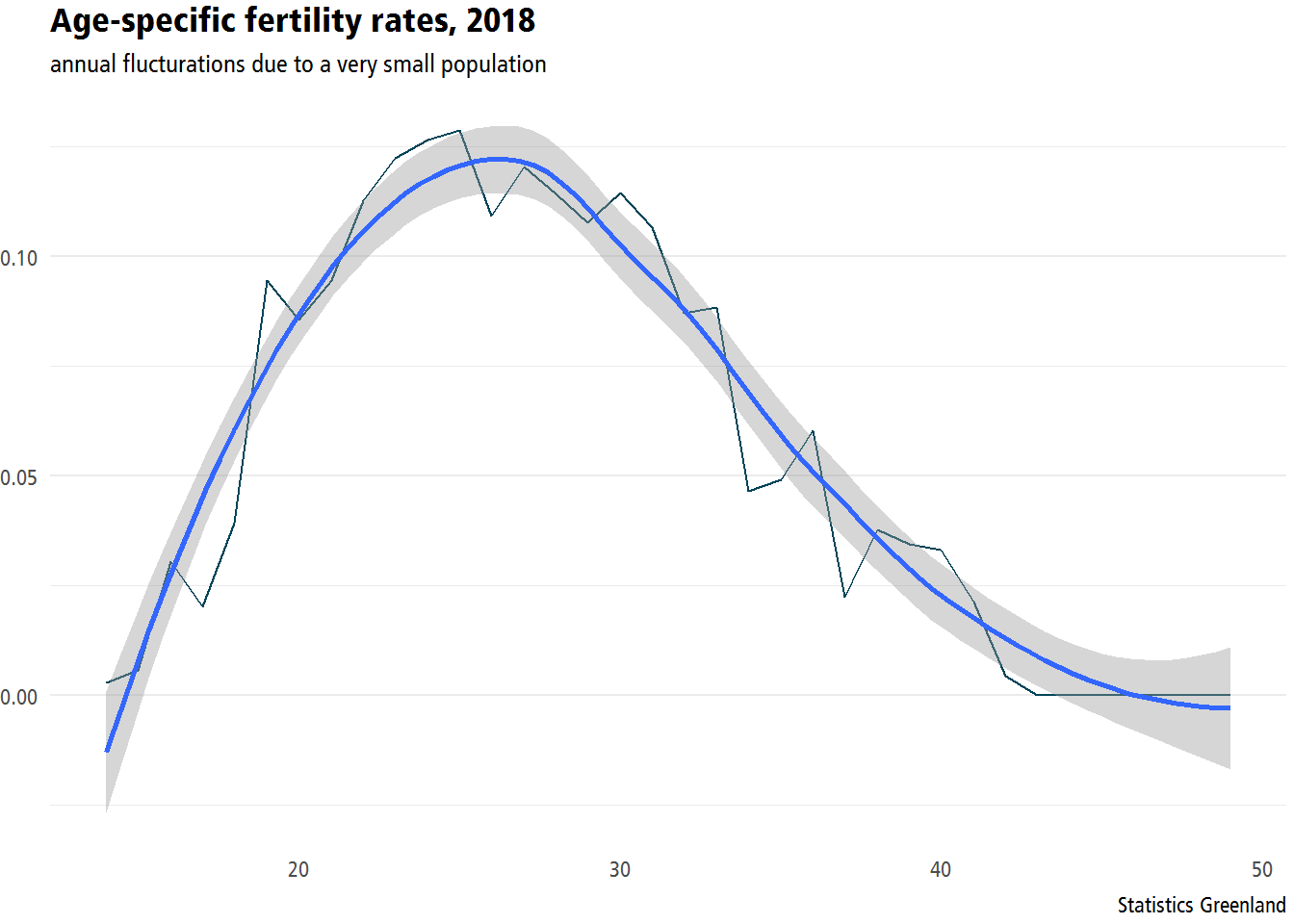
Often, when dealing with small areas fertility rates are calculated for more than one year, for instance 5-year average, in a Lexis diagram:
if(!require(LexisPlotR)){install.packages("LexisPlotR")}
library(LexisPlotR)
lexis3 <- lexis_grid(year_start = 2014, year_end = 2020, age_start = 22, age_end = 25)
polygons3 <- data.frame(group = c(1, 1, 1, 1),
x = c("2014-01-01", "2014-01-01", "2019-01-01", "2019-01-01"),
y = c(23, 24, 24, 23))
lexis_polygon(lg = lexis3, x = polygons3$x, y = polygons3$y, group = polygons3$group)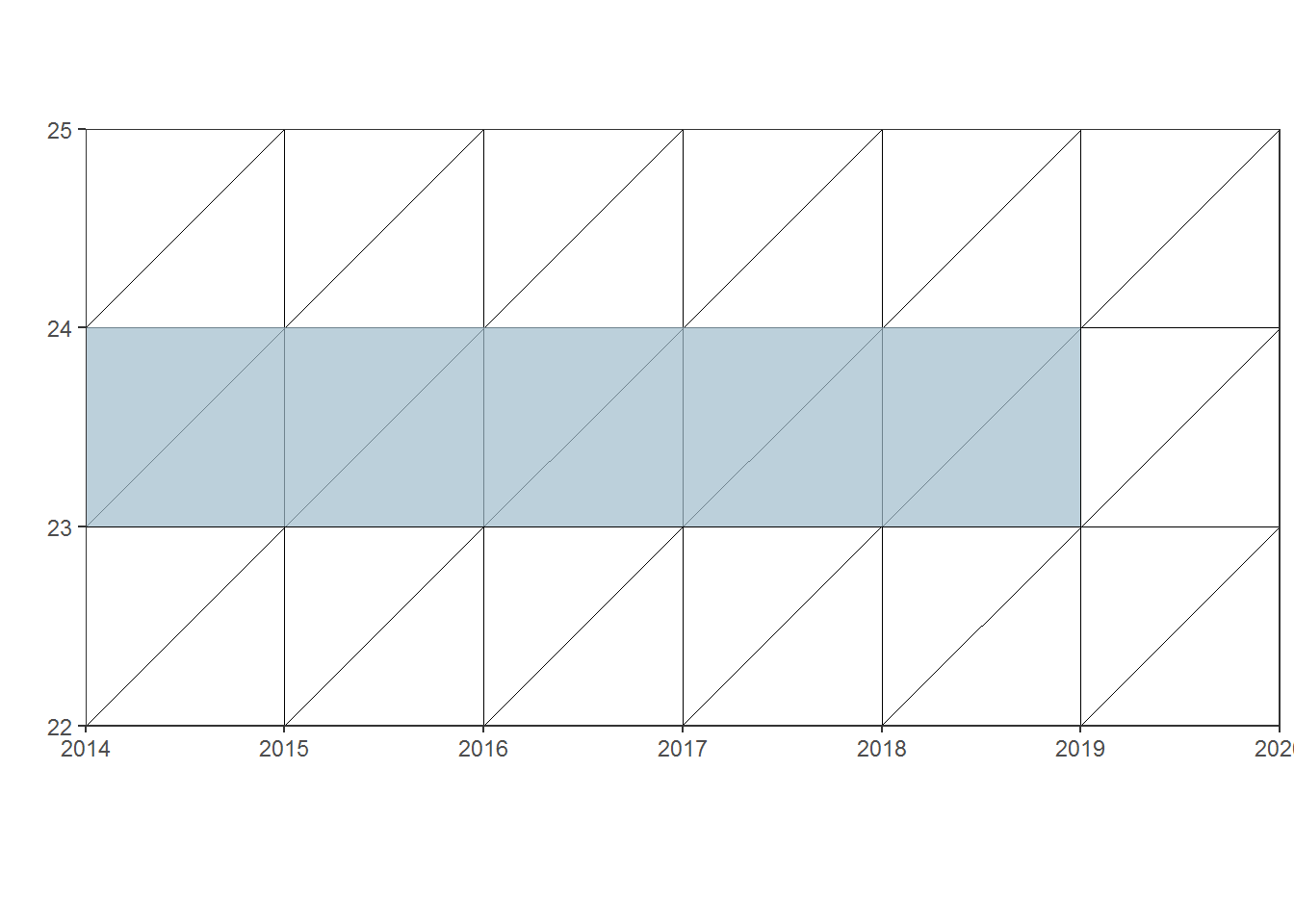
if(!require(LexisPlotR)){install.packages("LexisPlotR")}
library(LexisPlotR)
# Create a data.frame that contains the labels
labels5 <- data.frame(
x = c(
as.Date("2014-03-01"),
as.Date("2015-03-01"),
as.Date("2016-03-01"),
as.Date("2017-03-01"),
as.Date("2018-03-01"),
as.Date("2019-03-01"),
as.Date("2014-05-15"),
as.Date("2015-05-15"),
as.Date("2016-05-15"),
as.Date("2017-05-15"),
as.Date("2018-05-15"),
as.Date("2016-05-15"),
as.Date("2016-05-15"),
as.Date("2016-07-01")
),
y = c(
23.5,
23.5,
23.5,
23.5,
23.5,
23.5,
23.7,
23.7,
23.7,
23.7,
23.7,
24.3,
22.8,
22.6
),
label = c(
"438",
"411",
"436",
"395",
"402",
"399",
"birth: 48",
"birth: 43",
"birth: 49",
"birth: 49",
"birth: 49",
"livebirth 2014-18: 238=48+43+49+49+49",
"exposure 2014-18:",
"2062.5=(438/2)+411+436+395+402+(399/2)"
)
)
lexis5 <- lexis_grid(year_start = 2014, year_end = 2020, age_start = 22, age_end = 25)
# Use geom_text to plot the labels
lexis5 + geom_text(aes(x = labels5$x, y = labels5$y, label = labels5$label))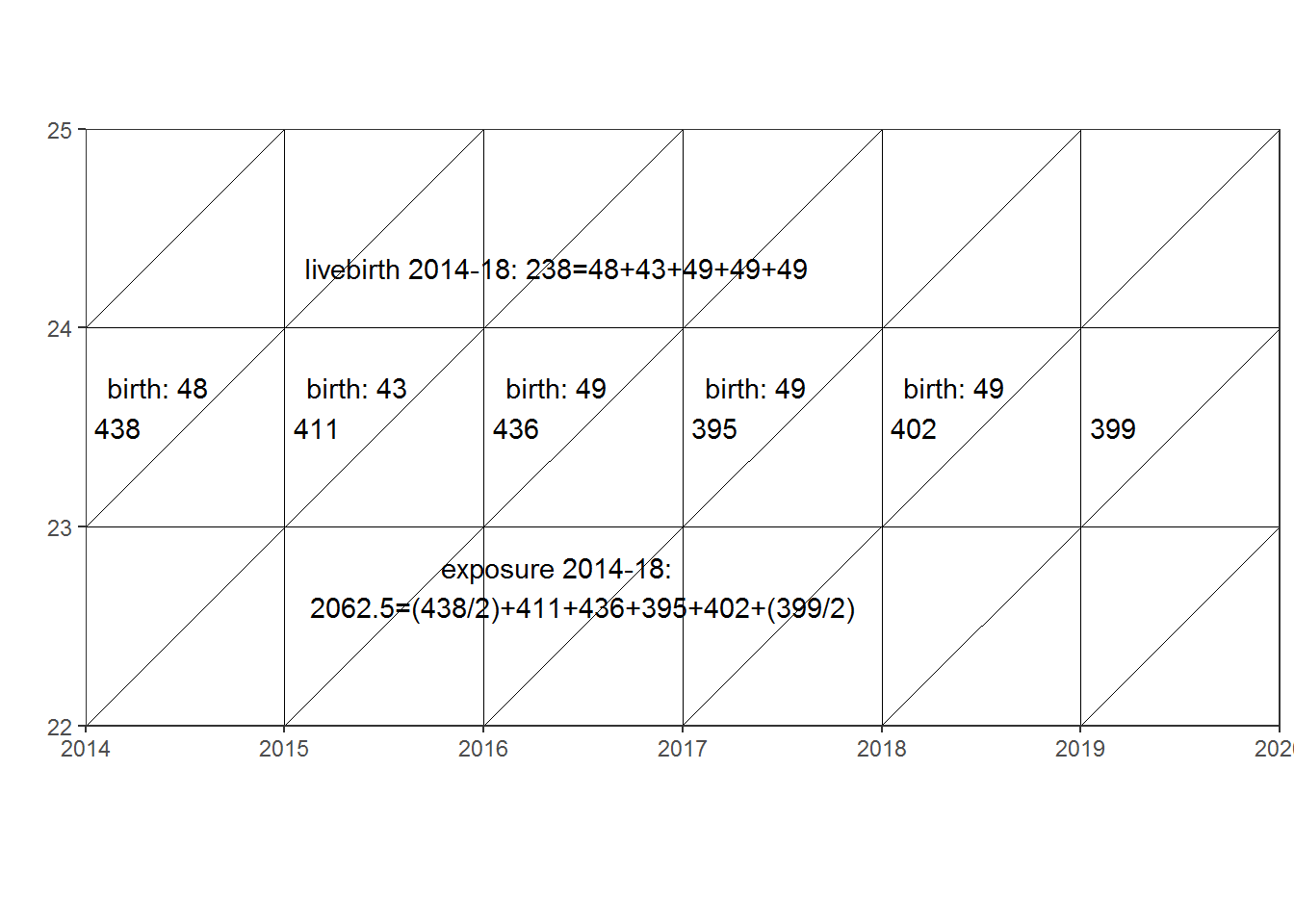
In this example an agespecific fertility rate for women aged 23 can be calculated as
0,11539 = 238/2062.5
#5 year fertility
#Birth 5 years a-groups
Ba<-BIRTHS2[,1:26]
#Ba <- Ba[,-c(2)]
Ba[,2:22]<-(Ba[,2:22]+Ba[,3:23]+Ba[,4:24]+Ba[,5:25]+Ba[,6:26])
Ba$age<-as.numeric(as.character(Ba$age))
#Ba <- Ba[,-c(23:26)]
#Exposure 5 years a-groups
EXPa<-POP_F[,1:27]
EXPa[,2:23]<-(POP_F[,2:23]/2+POP_F[,3:24]+POP_F[,4:25]+POP_F[,5:26]+POP_F[,6:27]/2)
EXPa$age<-as.numeric(as.character(EXPa$age))
#EXPa <- EXPa[,-c(23:27)]
ASFR2a<-Ba
ASFR2a[,2:22]<-Ba[,2:22]/EXPa[,2:22]
ASFR2a$age<-as.numeric(as.character(ASFR2a$age))
TFR2a<-colSums(ASFR2a[,2:26])
ASFR3a<-ASFR2a
ASFR3a[,2:26]<-ASFR3a[,2:26]*ASFR3a[,1]
MAB2a<-colSums(ASFR3a[,2:26])/TFR2a+0.5
ASFR223a <- filter(ASFR2a, age == '23')
ASFR23a<-colSums(ASFR223a[,2:22])
plot(ASFR23a, type="l", xlab="time", ylab="rate")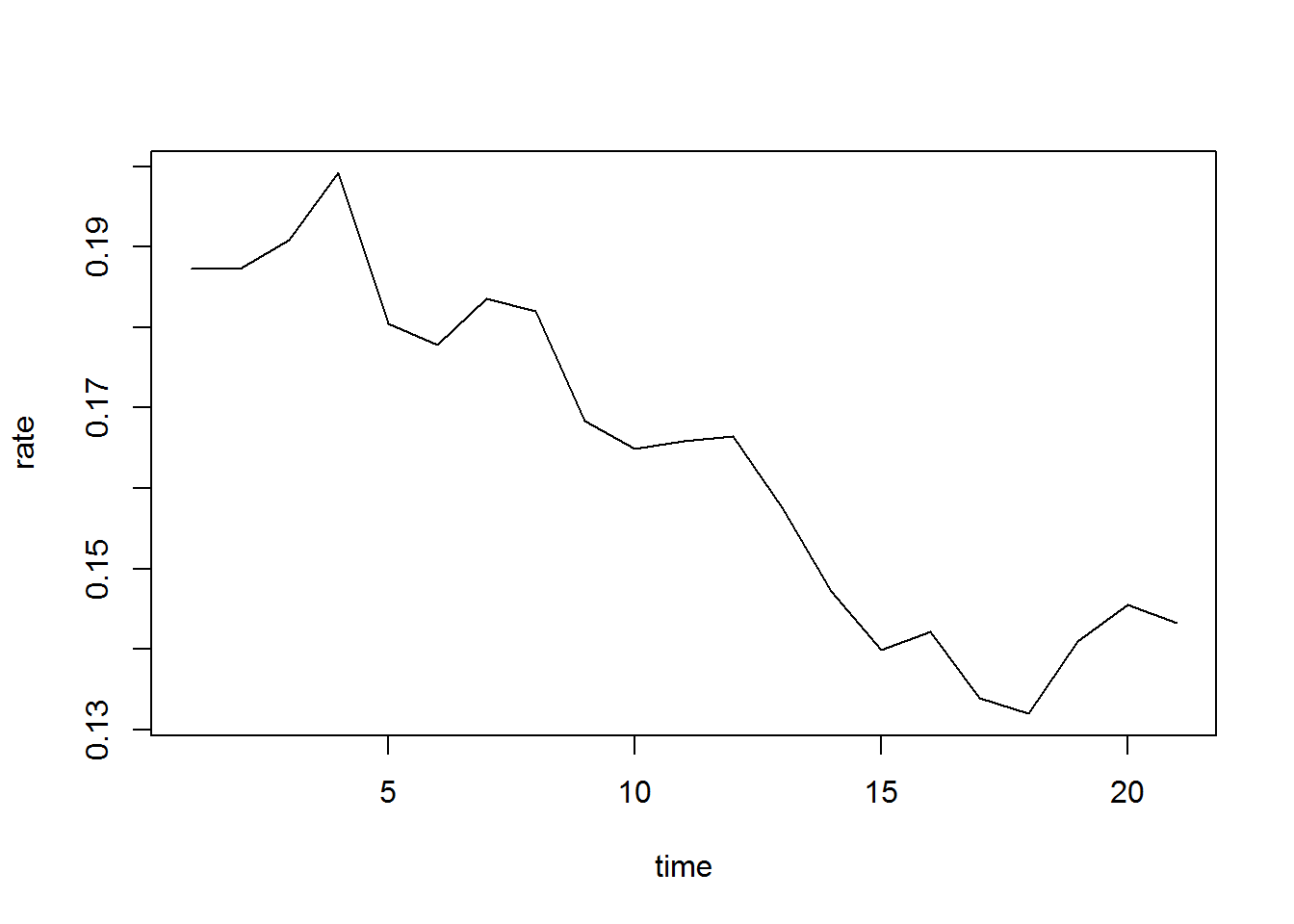
Total fertility rate
plot(TFR2, type="l", xlab="time", ylab="Total Fertility Rate ")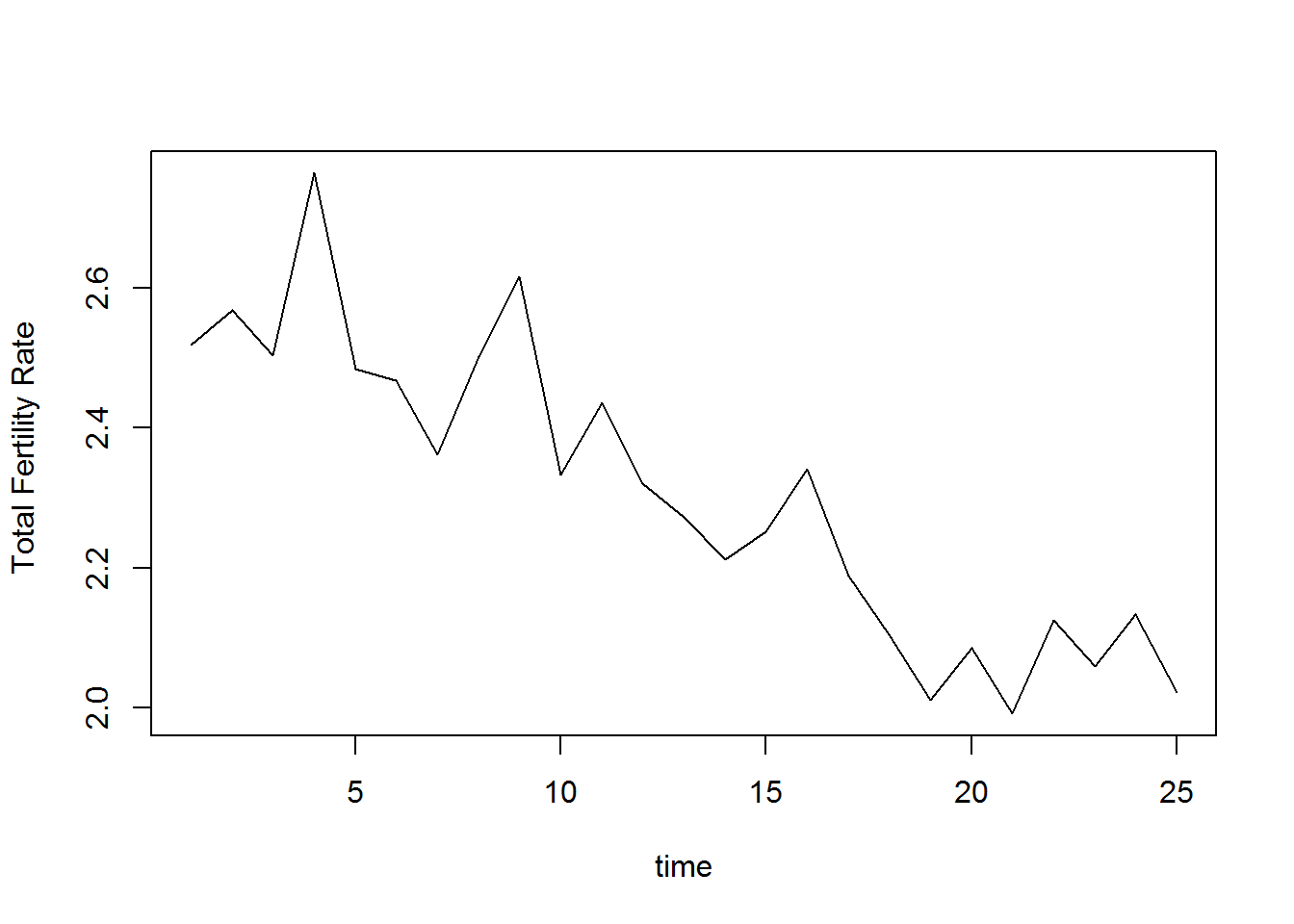
EXP2<-EXP[EXP$age>=14&EXP$age<=49,c(1,2:26)]
EXP_BO<-rbind(EXP2,EXP2,EXP2,EXP2,EXP2)
BIRTHS1 <- BIRTHS
BIRTHS1 <- BIRTHS1 %>% filter(BIRTHS1$`mothers place of birth` == "N")
BIRTHS1 <- subset(BIRTHS1, select = -`mothers place of birth`)
BIRTHS1$parity <- as.numeric(as.character(BIRTHS1$parity))
BIRTHS1$parity[BIRTHS1$parity>5]<-5
BIRTHS2<-subset(aggregate(BIRTHS1[,3:27],
list(as.numeric(as.character(BIRTHS1$`mothers age`)),BIRTHS1$parity),sum))
ASFR_BO<-BIRTHS2
ASFR_BO[,3:27]<-ASFR_BO[,3:27]/EXP_BO[,2:26]
TFR_BO<-aggregate(ASFR_BO[,3:27],
list(ASFR_BO$Group.2),sum)
ASFR_BO2<-ASFR_BO
ASFR_BO2[,3:27]<-ASFR_BO2[,3:27]*ASFR_BO[,1]
MAB_BO<-aggregate(ASFR_BO2[,3:27],
list(ASFR_BO2$Group.2),sum)
MAB_BO[,2:26]<-MAB_BO[,2:26]/TFR_BO[,2:26]+0.5
YLIM<-range(ASFR2[1:36,2:26])
YLIM2<-range(0,3) #range(TFR1[1,2:43])
YLIM3<-range(0,700) #range(TFR1[1,2:43])
AGES<-ASFR2[,1]
YEARS<-1977:2018
YEARS2<-1994:2018
YEARS3<-1973:2018
YEARSLast<-2018
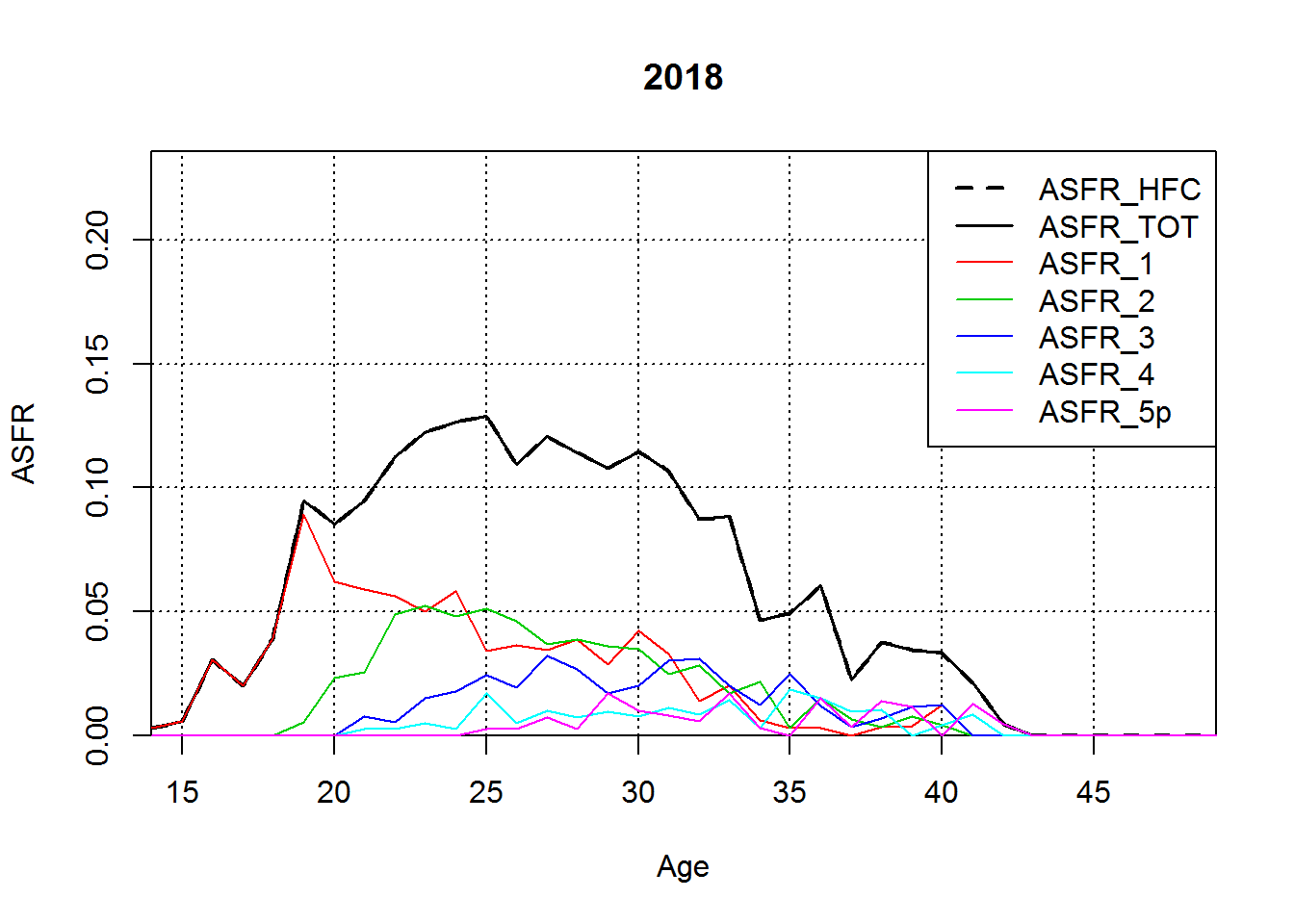
for(Y in YEARSLast){
plot(AGES,ASFR2[1:36,Y-1994+2],type="l",col=1,lwd=2,lty=2,
xlab="Age",ylab="ASFR",main=Y,
ylim=YLIM,xaxs="i",yaxs="i",
panel.first=grid(col=1))
if(Y>=YEARS2[1]){
lines(AGES,ASFR2[1:36,Y-1994+2],type="l",col=1,lwd=1.5,lty=1)
for(BO in 1:5){
lines(AGES,ASFR_BO[ASFR_BO$Group.2==BO,Y-1994+3],type="l",col=BO+1,lwd=1,lty=1)
}
}
legend("topright",paste("ASFR",c("HFC","TOT",1:4,"5p"),sep="_"),col=c(1,1:6),lwd=c(2,1.5,1,1,1,1,1),lty=c(2,1,1,1,1,1,1))
}
plot(MAB_BOGroup.1,MAB_BO[BO,2:26],type=“l”,col=BO+1,lwd=1,lty=1) }
legend(“topright”,paste(“ASFR”,c(“HFC”,“TOT”,1:4,“5p”),sep="_"),col=c(1,1:6),lwd=c(2,1.5,1,1,1,1,1),lty=c(2,1,1,1,1,1,1))
Mothers mean age at birth
plot(MAB2)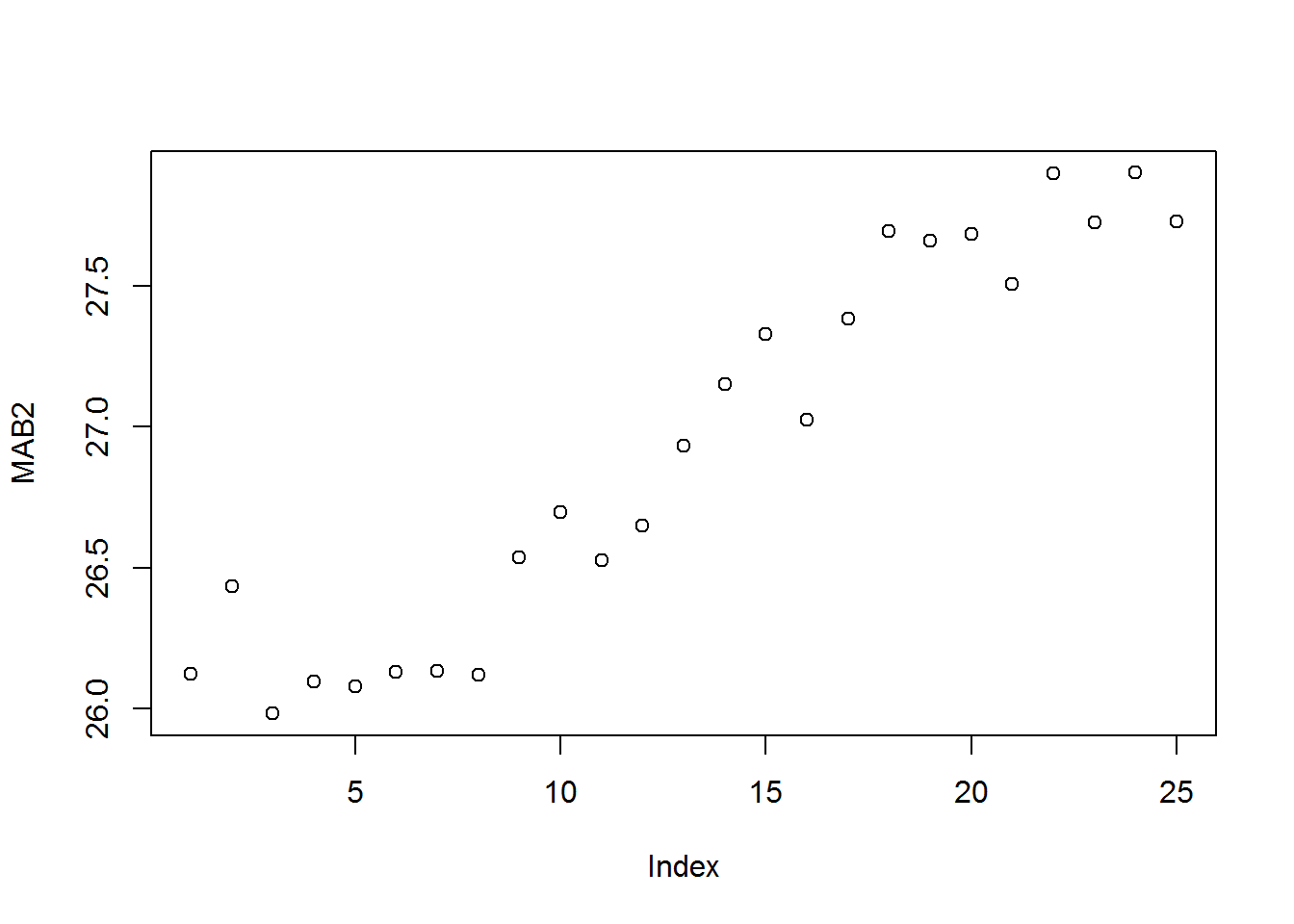
HFC OUTPUT
OUTPUTFILENAME<-“GRL_07_BO.csv” Country<-“GRL” Region<-NA Urban<-NA Origin<-NA
Year1<-rep(YEARS2,each=length(AGES)) Year2<-Year1 Age<-AGES AgeInt<-1 AgeDef<-“ACY” Vitality<-1
ASFR1<-as.vector(unlist(ASFR_BO[ASFR_BO$Group.2==1,3:27])) ASFR2<-as.vector(unlist(ASFR_BO[ASFR_BO$Group.2==2,3:27])) ASFR3<-as.vector(unlist(ASFR_BO[ASFR_BO$Group.2==3,3:27])) ASFR4<-as.vector(unlist(ASFR_BO[ASFR_BO$Group.2==4,3:27])) ASFR5P<-as.vector(unlist(ASFR_BO[ASFR_BO$Group.2==5,3:27]))
ASFR<-ASFR1+ASFR2+ASFR3+ASFR4+ASFR5P ASFR3P<-ASFR3+ASFR4+ASFR5P ASFR4P<-ASFR4+ASFR5P
Collection<-“RE” SourceType<-“estimate” RefCode<-“GRL_07” Note<-NA
OUTPUTDATA<-cbind(Country,Region,Urban,Origin,Year1,Year2,Age,AgeInt,AgeDef,Vitality, ASFR,ASFR1,ASFR2,ASFR3,ASFR3P,ASFR4,ASFR4P,ASFR5P, Collection,SourceType,RefCode,Note) OUTPUTDATA[,11:18]<-round(as.numeric(OUTPUTDATA[,11:18]),digits=5) OUTPUTFILENAME<-paste(RefCode,"_BO“,”.csv“,sep=”“) write.csv(OUTPUTDATA,file=OUTPUTFILENAME,na=”.",quote=FALSE,row.names=FALSE)
FINITO
author: “Lars Pedersen, larp@stat.gl - Statistics Greenland”
if(!require(“pxR”)){install.packages(“pxR”)} library(pxR) if(!require(“reshape2”)){install.packages(“reshape2”)} library(reshape2) # you should have at least three factor columns and one value column # so, artificially adding id as factor to further identify eruptions # and waiting time BIRTHS_pxw$id <- factor(seq.int(nrow(BIRTHS_pxw)))
then transform wide format data.frame (with 3 columns) into
narrow format data.frame
df <- melt(BIRTHS_pxw)
then to meet PX format requirement
add the copy of column variable
which identify either it “eruption” or “waiting”
dfvariable
converse to PX format
my_px <- as.px(df)
save PX-file
write.px(my_px, “my_px.px”)
https://lifeindenmark.borger.dk/Coming-to-Denmark/CPR-Bank-NemID/CPR---Registration-in-Denmark↩︎
Mainly electronic from 2019. It is possible to obtain access to microdata for researh & analysis. Learn more: http://betabank.stat.gl/pxweb/en/GSmicro/GSmicro__SU__GMFR89↩︎